小学校学校の授業(算数)とScratchプログラミングを組み合わせた問題に挑戦しましょう。
今回は、約分ツールを作ります。「約分なんか簡単にできる」という人にとってもプログラムを作るのは少し難しいかもしれません。
上の動画でも丁寧に解説しています。
この記事では、プログラミングを作るうえでの考えかたも合わせて解説していきます。
約分をおさらい
プログラムを作る前に、約分についてしっかり理解しておく必要があります。
約分についておさらいしましょう。
約分は、分母と分子の最大公約数で分母・分子を割ってあげます。
例えば \(\frac{4}{8} \) を約分する場合は、分母の8、分子の4をそれぞれ4で割って
\(\frac{1}{2} \) となります。
( 最大公約数で割らなくても、\(\frac{4}{8} \) を2で割ってみて \(\frac{2}{4} \)
さらに2で割って、 \(\frac{1}{2} \) と、とにかく割れる数で割ってみることでも約分ができますが。
今回のプログラムでは、最大公約数で割るという考え方を使います。)
コンピュータは約分をしらない
約分を知っている人に、約分をお願いするときは
「約分をして」とお願いすれば、やってほしいことが伝わります。
しかし、コンピュータに「約分して」とお願いしても、何もしてくれません。
さらに言えば、「分母と分子を最大公約数で割って」とお願いしても何もしてくれません。
分母って?分子って?最大公約数って?コンピュータは知らないことばかりです。
最大公約数で割る手順(約分する手順)を整理
まず、分母・分子の最大公約数の求め方を考えましょう。
求め方はいろいろありますが、今回はシンプルに考えていきます。

分母・分子の最大公約数は、必ず分母・分子よりも小さい数です。
(例えば、 \(\frac{4}{8} \) なら、4よりも小さい)
これは、自分より大きい数では割り切れないので当然ですね。(例:4は5で割れない。)
なので、まずは分母・分子の小さいほうで、約分してみましょう。
\(\frac{4}{8} \) の場合は、分子のほうが小さいので、4で分母分子を割ってみましょう。
この場合は、割り切れたので、約分完了です。
\(\frac{6}{10} \)の場合、分子のほうが小さいので、6で分母分子を割ってみましょう。
このとき、分母の10は割り切ることができないので、約分できません。
その時は、割る数を1減らして、5で割ってみましょう。今度は分子の6が割り切れません。
また1減らして4で割ってみても、3で割ってみても、割り切れません。
さらに1減らして、2の場合は分母も分子も割り切ることができるので、約分完了です。

大きい数から順番に1ずつ減らしてわっていけば、必ず最大公約数が見つかりますね!
実際、人が計算するときはこの方法だと手間ですが、コンピュータは繰り返し処理が得意なのであっという間に実行してくれます。
手順の整理
- 分母と分子の小さいほうを割る数にする
- 割る数で分母分子を割ってみる
- 割り切れたら、約分完了
- 割り切れなかったら、割る数を1減らして、(2.)の手順に戻る
プログラムを作る
手順をもとにプログラミングしていきます。

割る数を分子に設定して、分母分子が割り切れえるまで割る数を1ずつ減らしていき、
割り切れる数が見つかったら最後に約分してくれます。
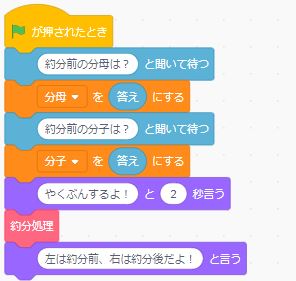
約分処理がプログラミングできたら、分数の入力を受付けるプログラムを書いて完成です!
(詳細は動画を見てみてください!)
お疲れさまでした!最後までお読みいただきありがとうございます。
↓その他おすすめ問題