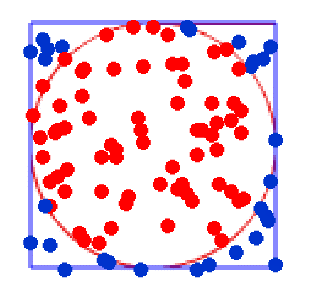
モンテカルロ法で円の面積を求める方法と仕組みをシンプルに解説します。
モンテカルロ法とは、乱数を使って数値計算を行う手法の総称です。この乱数を使う発想を利用して円の面積を求めます。
モンテカルロ法とは
円の面積といえば?

半径 × 半径 × 3.14(円周率)!
そうです。
ただし、これは円周率が3.14だとした場合の公式です。
もし、円周率がわからなかったら円の面積は求めることができません。
しかし、モンテカルロ法を用いることで円周率を使わないでも
円の面積を求めることができます。

円周率わかってるのに、モンテカルロ法って意味ある???
そう思うかもしれませんが、実はモンテカルロ法は円の面積だけでなく
公式などが適用できないどんな形の図形でも面積を求められます。
今回は、わかりやすいように円の面積を求める方法を例にモンテカルロ法を説明していきますが
考え方がわかればいろいろな問題に拡張できます。
モンテカルロ法で面積が求められる原理
モンテカルロ法により面積が求まる過程を説明します。
例:直径10cmの円の面積を求める場合(以下あえて単位はつけません)
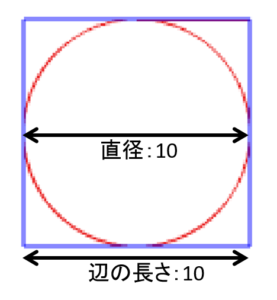
このような、1辺10の正方形とそれに内接する直径10の円があったとします。
この正方形の面積は、1辺が10の正方形なので
面積100ですね。
では、この正方形の中のランダムな位置にたくさんの点を打ち込みます。
100個の点を打ってみると、例えば下の図のようになります。
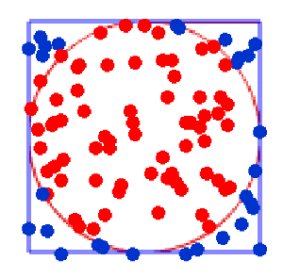

円の中に打たれた点は赤色、円の外側に打たれた点は青色になっているね。
はい、では 円の中に打たれた点の数(赤色の点)を数えます。
この場合、赤色の点は71個ありました。
100個中71個が円の中にあるということは、赤色の点が打たれる確率は71%です。
この確率から面積を求めます。
正方形の中にランダムに点をうったら71%の確率で円の中に点が打たれるということは、
円は正方形の71%の面積を占めていると考えることができます。

ということは、正方形の面積(100)の71%だから
円の面積は71ということになるね。
はい、これでモンテカルロ法で円を求めることができました。考え方はシンプルですよね!
では、実際に円の公式(半径×半径×3.14)で求めた円の面積と比較してみます。
円の公式で求めた面積:5×5×3.14=78.5
モンテカルロ法で求めた面積:100×71%=71

あってないじゃん!!!
そうなんです、モンテカルロ法は実際の答えとずれてしまう場合があるのです。
面積を求める過程でランダムに点を配置していますよね。これが原因です。
偶然円の中に点が偏ることもあれば、円の外側に偏ることもあります。
この偏りによって、正確な答えとずれが出てきてしまいます。
しかし、対策があります!
それは・・・点をめちゃくちゃ増やします!
点をめちゃくちゃ増やすことで、確率が収束し真の答えに近づきます。
今回の例では点の数は100でやりましたが、全然足りません。
もっと1000、10000と大きくすればするほど、真の答えに近づきます。
(増やすしすぎると計算時間が膨大になるので、計算時間と答えの正確さはトレードオフです。)
Scratchで実装してみた
モンテカルロ法による面積を求めるプログラムをScratchを使って実装してみました。
今回の記事で説明した仕組み をそのままプログラムにしています。このプログラムでは点の数は300としています。
以上、最後までお読みいただきありがとうございました。
↓円周率を求めてみる問題